Winning a Kaggle Competition in Python - Part 2
Now that you know the basics of Kaggle competitions, you will learn how to study the specific problem at hand. You will practice EDA and get to establish correct local validation strategies. You will also learn about data leakage.
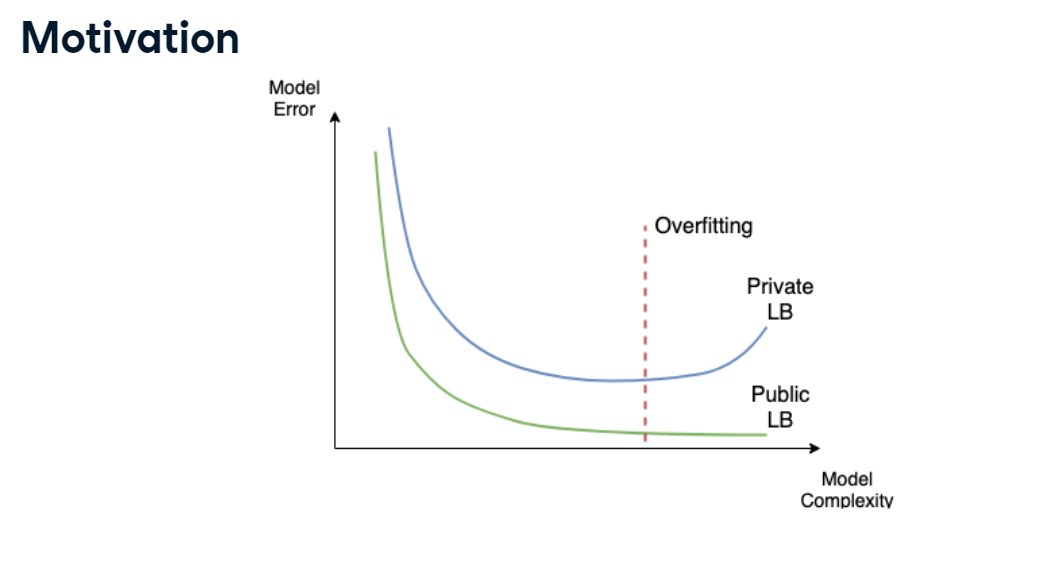
Understand the problem
- Solution workflow

- Data type: tabular data, time series, images, text, etc.
- Problem type: classification, regression, ranking, etc.
Evalation Metrics: ROC AUC, F1-Score, MAE, MSE, etc.
Example Custom Metric (Root Mean Squared Error in a Logarithmic scale):
$$ RMSLE = \sqrt{\frac{1}{N}\sum_{i=1}^N (\log(y_i + 1) - \log(\hat{y_i} + 1))^2} $$
- Define a competition metrics

import numpy as np
import pandas as pd
# Import log_loss from sklearn
from sklearn.metrics import log_loss
# Define your own LogLoss function
def own_logloss(y_true, prob_pred):
# Find loss for each observation
terms = y_true * np.log(prob_pred) + (1 - y_true) * np.log(1 - prob_pred)
# Find mean over all observations
err = np.mean(terms)
return -err
y_classification_true = np.array([ 1, 1, 0, 1, 0, 1, 1, 1, 0, 1, 1, 1, 1, 1, 0, 0, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 0, 0, 1, 1, 1, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0,
0, 0, 1, 0, 1, 0, 1, 0, 0, 0, 0, 1, 1, 0, 1, 0, 1, 0, 1, 1, 1, 0,
1, 0, 0, 0, 0, 1, 1, 1, 0, 0, 0, 1, 1, 1, 0, 0, 0, 0, 1, 0, 1, 1,
0, 1, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0])
y_classification_pred = np.array([ 0.2082483 , 0.4433677 , 0.71560128, 0.41051979, 0.19100696,
0.96749431, 0.65075037, 0.86545985, 0.02524236, 0.26690581,
0.5020711 , 0.06744864, 0.99303326, 0.2364624 , 0.37429218,
0.21401191, 0.10544587, 0.23247979, 0.30061014, 0.63444227,
0.28123478, 0.36227676, 0.00594284, 0.36571913, 0.53388598,
0.16201584, 0.59743311, 0.29315247, 0.63205049, 0.02619661,
0.88759346, 0.01611863, 0.12695803, 0.77716246, 0.04589523,
0.71099869, 0.97104614, 0.87168293, 0.71016165, 0.95850974,
0.42981334, 0.87287891, 0.35595767, 0.92976365, 0.14877766,
0.94002901, 0.8327162 , 0.84605484, 0.12392301, 0.5964869 ,
0.01639248, 0.72118437, 0.00773751, 0.08482228, 0.22549841,
0.87512453, 0.36357632, 0.53995994, 0.56810321, 0.22546336,
0.57214677, 0.6609518 , 0.29824539, 0.41862686, 0.45308892,
0.93235066, 0.58749375, 0.94825237, 0.55603475, 0.50056142,
0.00353221, 0.48088904, 0.927455 , 0.19836569, 0.05209113,
0.40677889, 0.37239648, 0.85715306, 0.02661112, 0.92014923,
0.680903 , 0.90422599, 0.60752907, 0.81195331, 0.33554387,
0.34956623, 0.38987423, 0.75479708, 0.36929117, 0.24221981,
0.93766836, 0.90801108, 0.34879732, 0.63463807, 0.27384221,
0.20611513, 0.33633953, 0.32709989, 0.8822761 , 0.82230381])
print('Your LogLoss: {:.5f}'.format(own_logloss(y_classification_true, y_classification_pred)))
print('Sklearn LogLoss: {:.5f}'.format(log_loss(y_classification_true, y_classification_pred)))
Initial EDA
Goals of EDA:
- Size of the data
- Properties of the target variable
- Properties of the features
- Generate ideas for feature engineering
Example - Two sigma connect rental listing inquiries:
- Predict the popularity of an apartment rental listing
- target variable: interest_level
- Problem type: Classification ( 3 classes: 'high', 'medium', 'low' )
- Metric: Multi-class log loss
EDA. Part I
import pandas as pd
twosigma_train = pd.read_json(open("datasets/two_sigma_connect/train.json"))
twosigma_test = pd.read_json(open("datasets/two_sigma_connect/test.json"))
print('Train shape:', twosigma_train.shape)
print('Test shape:', twosigma_test.shape)
print(twosigma_train.columns.tolist())
twosigma_train.rename(columns={'listing_id':'id'}, inplace=True)
twosigma_test.rename(columns={'listing_id':'id'}, inplace=True)
TO_KEEP = ['bathrooms', 'bedrooms', 'building_id', 'latitude', 'id', 'longitude', 'manager_id', 'price', 'interest_level']
for col in twosigma_train.columns.tolist():
if col not in TO_KEEP:
twosigma_train.drop([col], axis = 1, inplace = True)
twosigma_test.drop([col], axis = 1, inplace = True)
print(twosigma_train.columns.tolist())
print(twosigma_train.interest_level.value_counts())
twosigma_train.set_index('id', inplace = True)
twosigma_test.set_index('id', inplace = True)
twosigma_train.describe()
twosigma_train.head(10)
import matplotlib.pyplot as plt
plt.style.use('ggplot')
# find the median price by the interest level
prices = twosigma_train.groupby('interest_level', as_index=False)['price'].median()
fig = plt.figure(figsize=(7,5))
plt.bar(prices.interest_level, prices.price, width=0.5, alpha = 0.8)
plt.xlabel('Interest level')
plt.ylabel('Median price')
plt.title('Median listing price across interest level')
plt.show()
""" This shows that lower median price get high interest level, while higher prices get low interest level. """
twosigma_train.interest_level.value_counts()
EDA Statistic
As mentioned in the slides, you'll work with New York City taxi fare prediction data. You'll start with finding some basic statistics about the data. Then you'll move forward to plot some dependencies and generate hypotheses on them.
The train and test DataFrames are already available in your workspace.
Instructions:
- Describe the "fare_amount" column to get some statistics about the target variable.
- Find the distribution of the "passenger_count" in the train data (using the value_counts() method).
pd.set_option('display.expand_frame_repr', False)
# Read train data
train = pd.read_csv('datasets/taxi_train_chapter_4.csv')
test = pd.read_csv('datasets/taxi_test_chapter_4.csv')
# Shapes of train and test data
print('Train shape:', train.shape)
print('Test shape:', test.shape)
# Train head()
display(train.head().style.applymap(lambda x:'white-space:nowrap'))
# Describe the target variable
print(train.fare_amount.describe())
# Train distribution of passengers within rides
print(train.passenger_count.value_counts())
EDA plots I
After generating a couple of basic statistics, it's time to come up with and validate some ideas about the data dependencies. Again, the train DataFrame from the taxi competition is already available in your workspace.
To begin with, let's make a scatterplot plotting the relationship between the fare amount and the distance of the ride. Intuitively, the longer the ride, the higher its price.
To get the distance in kilometers between two geo-coordinates, you will use Haversine distance. Its calculation is available with the haversine_distance() function defined for you. The function expects train DataFrame as input.
Instructions:
- Create a new variable "distance_km" as Haversine distance between pickup and dropoff points.
- Plot a scatterplot with "fare_amount" on the x axis and "distance_km" on the y axis. To draw a scatterplot use matplotlib scatter() method.
- Set a limit on a ride distance to be between 0 and 50 kilometers to avoid plotting outliers.
def haversine_distance(train):
""" Define Haversine distance """
data = [train]
lat1, long1, lat2, long2 = 'pickup_latitude', 'pickup_longitude', 'dropoff_latitude', 'dropoff_longitude'
for i in data:
R = 6371 #radius of earth in kilometers
#R = 3959 #radius of earth in miles
phi1 = np.radians(i[lat1])
phi2 = np.radians(i[lat2])
delta_phi = np.radians(i[lat2]-i[lat1])
delta_lambda = np.radians(i[long2]-i[long1])
#a = sin²((φB - φA)/2) + cos φA . cos φB . sin²((λB - λA)/2)
a = np.sin(delta_phi / 2.0) ** 2 + np.cos(phi1) * np.cos(phi2) * np.sin(delta_lambda / 2.0) ** 2
#c = 2 * atan2( √a, √(1−a) )
c = 2 * np.arctan2(np.sqrt(a), np.sqrt(1-a))
#d = R*c
d = (R * c) #in kilometers
return d
train['distance_km'] = haversine_distance(train)
# Draw a scatterplot
plt.scatter(x=train["fare_amount"], y=train["distance_km"], alpha=0.5)
plt.xlabel('Fare amount')
plt.ylabel('Distance, km')
plt.title('Fare amount based on the distance')
# Limit on the distance
plt.ylim(0, 50)
plt.show()
Nice plot! It's obvious now that there is a clear dependency between ride distance and fare amount. So, ride distance is, probably, a good feature. Let's find some others!
EDA plots II
Another idea that comes to mind is that the price of a ride could change during the day.
Your goal is to plot the median fare amount for each hour of the day as a simple line plot. The hour feature is calculated for you. Don't worry if you do not know how to work with the date features. We will explore them in the chapter on Feature Engineering.
Instructions:
- Group train DataFrame by "hour" and calculate the median for the "fare_amount" column.
- Using hour_price DataFrame obtained, plot a line with "hour" on the x axis and "fare_amount" on the y axis.
train['pickup_datetime'] = pd.to_datetime(train.pickup_datetime)
train['hour'] = train.pickup_datetime.dt.hour
# Find median fare_amount for each hour
hour_price = train.groupby('hour', as_index=False)['fare_amount'].median()
# Plot the line plot
plt.plot(hour_price['hour'], hour_price['fare_amount'], marker='o')
plt.xlabel('Hour of the day')
plt.ylabel('Median fare amount')
plt.title('Fare amount based on day time')
plt.xticks(range(24))
plt.show()
Great! We see that prices are a bit higher during the night. It is a good indicator that we should include the "hour" feature in the final model, or at least add a binary feature "is_night". Move on to the next lesson to learn how to check whether new features are useful for the model or not!
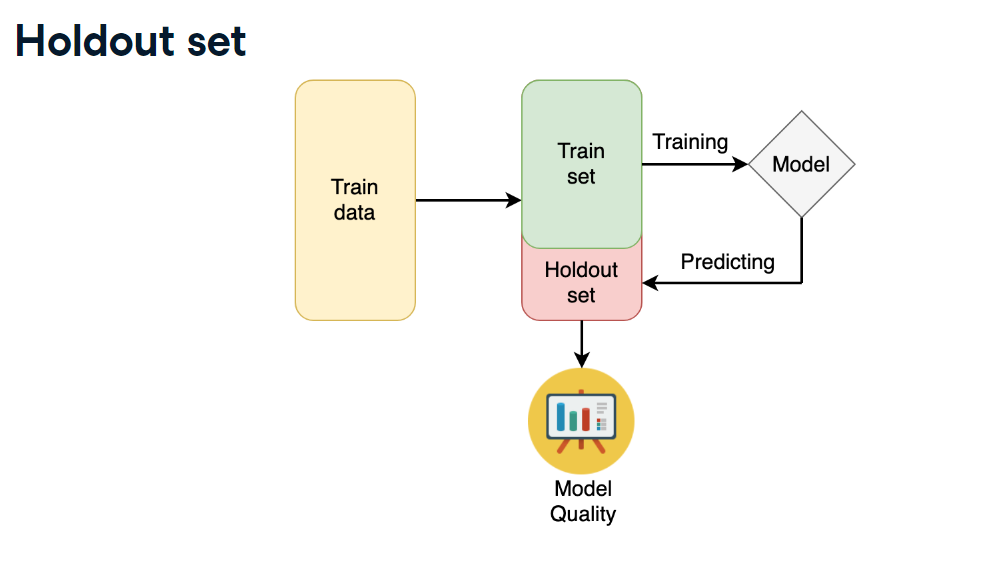
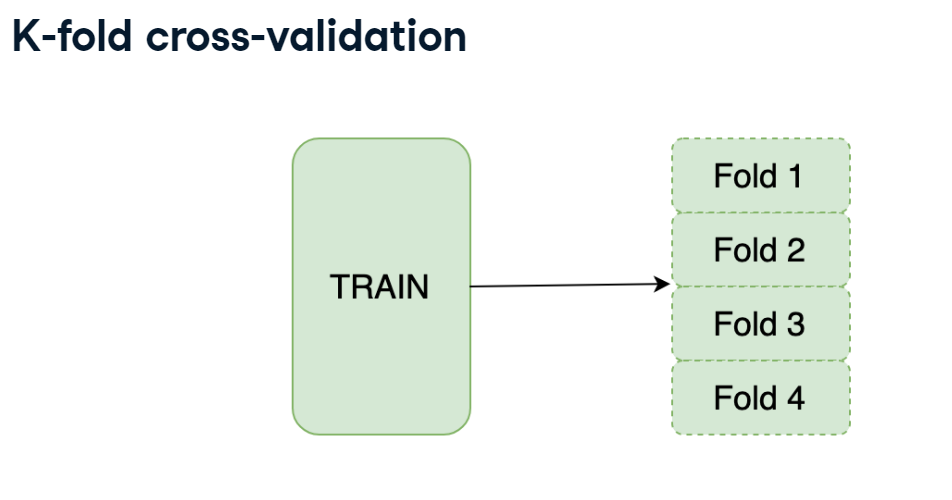
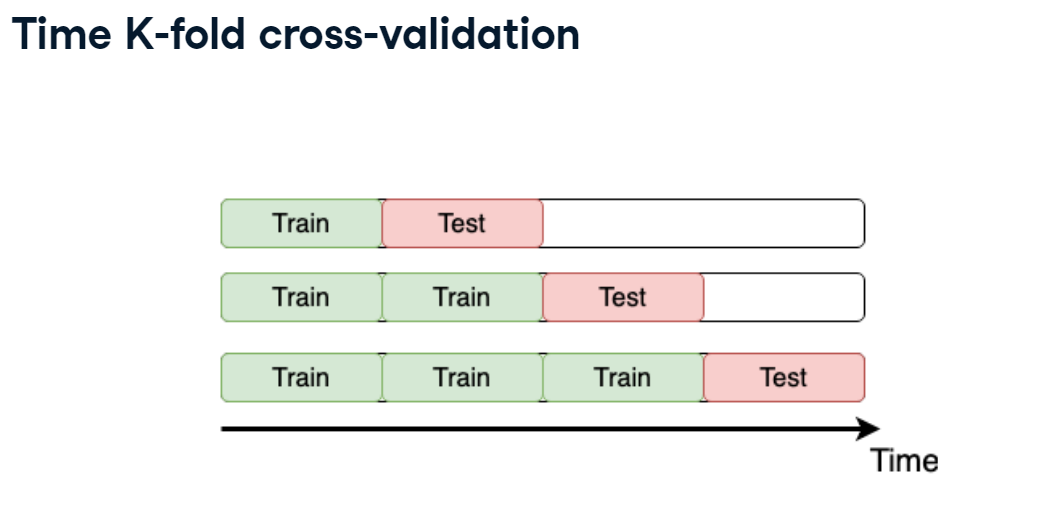
K-fold cross-validation
You will start by getting hands-on experience in the most commonly used K-fold cross-validation.
The data you'll be working with is from the "Two sigma connect: rental listing inquiries" Kaggle competition. The competition problem is a multi-class classification of the rental listings into 3 classes: low interest, medium interest and high interest. For faster performance, you will work with a subsample consisting of 1,000 observations.
You need to implement a K-fold validation strategy and look at the sizes of each fold obtained. train DataFrame is already available in your workspace.
Instructions:
- Create a KFold object with 3 folds.
- Loop over each split using the kf object.
- For each split select training and testing folds using train_index and test_index.
from sklearn.model_selection import KFold
# Create a KFold object
kf = KFold(n_splits=3, shuffle=True, random_state=123)
# subsample 1000
sub_train = twosigma_train.sample(n = 1000)
# Loop through each split
fold = 0
for train_index, test_index in kf.split(sub_train):
# print(train_index, test_index)
# Obtain training and testing folds
cv_train, cv_test = sub_train.iloc[train_index], sub_train.iloc[test_index]
print('Fold: {}'.format(fold))
print('CV train shape: {}, CV test shape: {}'.format(cv_train.shape, cv_test.shape))
print('Medium interest listings in CV train: {}'.format(sum(cv_train.interest_level == 'medium')))
print('Medium interest listings in CV test: {}\n'.format(sum(cv_test.interest_level == 'medium')))
fold += 1
So, we see that the number of observations in each fold is almost uniform. It means that we've just splitted the train data into 3 equal folds. However, if we look at the number of medium-interest listings, it's varying from 162 to 175 from one fold to another. To make them uniform among the folds, let's use Stratified K-fold!
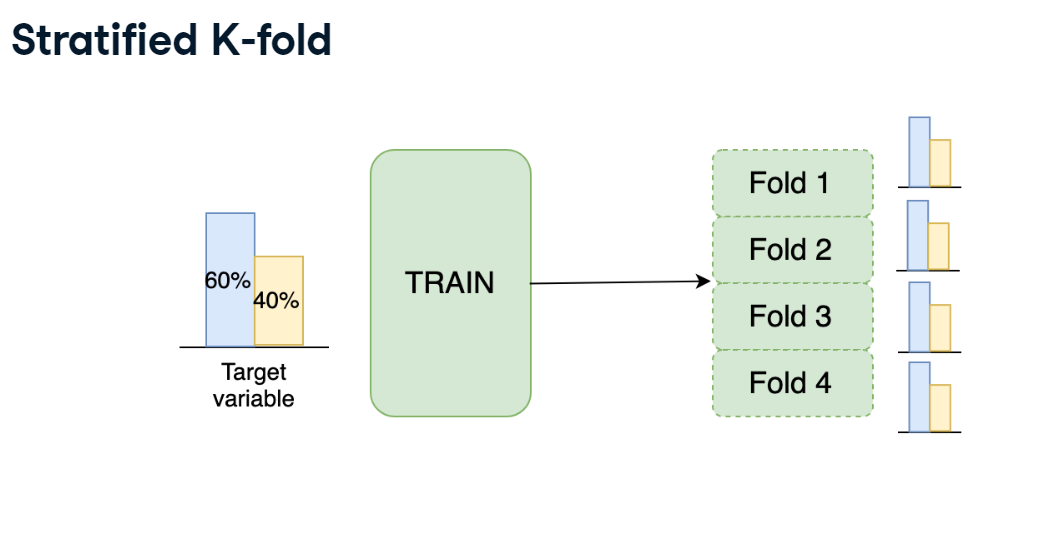
Stratified K-fold
As you've just noticed, you have a pretty different target variable distribution among the folds due to the random splits. It's not crucial for this particular competition, but could be an issue for the classification competitions with the highly imbalanced target variable.
To overcome this, let's implement the stratified K-fold strategy with the stratification on the target variable. train DataFrame is already available in your workspace.
Instructions:
- Create a StratifiedKFold object with 3 folds and shuffling.
- Loop over each split using str_kf object. Stratification is based on the "interest_level" column.
- For each split select training and testing folds using train_index and test_index.
from sklearn.model_selection import StratifiedKFold
# Create a StratifiedKFold object
str_kf = StratifiedKFold(n_splits=3, shuffle=True, random_state=123)
# subsample 1000
sub_train = twosigma_train.sample(n = 1000)
# Loop through each split
fold = 0
for train_index, test_index in str_kf.split(sub_train, sub_train['interest_level']):
# Obtain training and testing folds
cv_train, cv_test = sub_train.iloc[train_index], sub_train.iloc[test_index]
print('Fold: {}'.format(fold))
print('CV train shape: {}, CV test shape: {}'.format(cv_train.shape, cv_test.shape))
print('Medium interest listings in CV train: {}'.format(sum(cv_train.interest_level == 'medium')))
print('Medium interest listings in CV test: {}\n'.format(sum(cv_test.interest_level == 'medium')))
fold += 1
Great! Now you see that both size and target distribution are the same among the folds. The general rule is to prefer Stratified K-Fold over usual K-Fold in any classification problem. Move to the next lesson to learn about other cross-validation strategies!
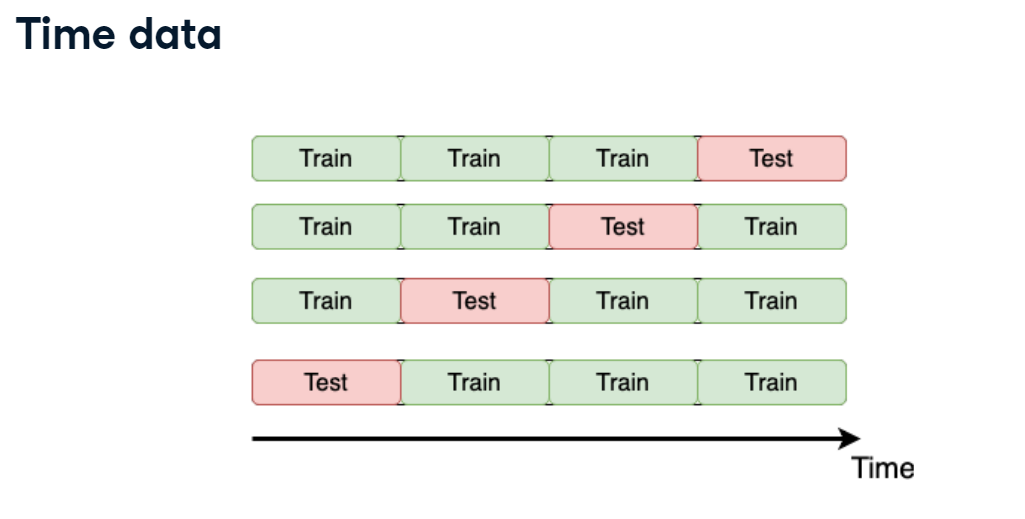
Time K-fold
Remember the "Store Item Demand Forecasting Challenge" where you are given store-item sales data, and have to predict future sales?
It's a competition with time series data. So, time K-fold cross-validation should be applied. Your goal is to create this cross-validation strategy and make sure that it works as expected.
Note that the train DataFrame is already available in your workspace, and that TimeSeriesSplit has been imported from sklearn.model_selection.
Instructions:
- Create a TimeSeriesSplit object with 3 splits.
- Sort the train data by "date" column to apply time K-fold.
- Loop over each time split using time_kfold object.
- For each split select training and testing folds using train_index and test_index.
from sklearn.model_selection import TimeSeriesSplit
train_df = pd.read_csv("datasets/demand_forecasting_train_1_month.csv")
# Create TimeSeriesSplit object
time_kfold = TimeSeriesSplit(n_splits=3)
# Sort train data by date
train = train_df.sort_values('date')
# Iterate through each split
fold = 0
for train_index, test_index in time_kfold.split(train):
cv_train, cv_test = train.iloc[train_index], train.iloc[test_index]
print('Fold :', fold)
print('Train date range: from {} to {}'.format(cv_train.date.min(), cv_train.date.max()))
print('Test date range: from {} to {}\n'.format(cv_test.date.min(), cv_test.date.max()))
fold += 1
Great! You've applied time K-fold cross-validation strategy for the demand forecasting. Look at the output. It works as expected, training only on the past data and predicting the future. Progress to the next exercise to evaluate different models!
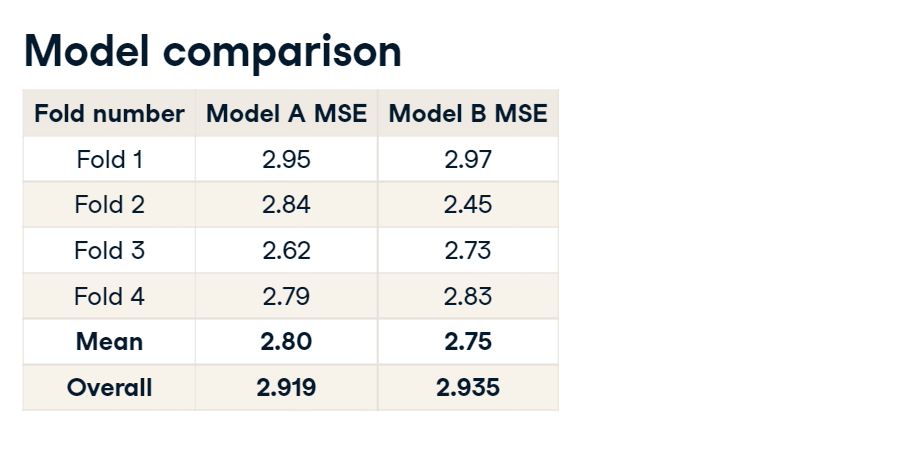
Overall validation score
Now it's time to get the actual model performance using cross-validation! How does our store item demand prediction model perform?
Your task is to take the Mean Squared Error (MSE) for each fold separately, and then combine these results into a single number.
For simplicity, you're given get_fold_mse() function that for each cross-validation split fits a Random Forest model and returns a list of MSE scores by fold. get_fold_mse() accepts two arguments: train and TimeSeriesSplit object.
Instructions 1/3
- Create time 3-fold cross-validation.
- Print the numpy mean of MSE scores by folds.
from sklearn.ensemble import RandomForestRegressor
from sklearn.metrics import mean_squared_error
def get_fold_mse(train, kf):
mse_scores = []
for train_index, test_index in kf.split(train):
fold_train, fold_test = train.loc[train_index], train.loc[test_index]
# Fit the data and make predictions
# Create a Random Forest object
rf = RandomForestRegressor(n_estimators=10, random_state=123)
# Train a model
rf.fit(X=fold_train[['store', 'item']], y=fold_train['sales'])
# Get predictions for the test set
pred = rf.predict(fold_test[['store', 'item']])
fold_score = round(mean_squared_error(fold_test['sales'], pred), 5)
mse_scores.append(fold_score)
return mse_scores
from sklearn.model_selection import TimeSeriesSplit
import numpy as np
# Sort train data by date
train = train.sort_values('date')
# Initialize 3-fold time cross-validation
kf = TimeSeriesSplit(n_splits=3)
# Get MSE scores for each cross-validation split
mse_scores = get_fold_mse(train, kf)
print('Mean validation MSE: {:.5f}'.format(np.mean(mse_scores)))
print('MSE by fold: {}'.format(mse_scores))
print('Overall validation MSE: {:.5f}'.format(np.mean(mse_scores) + np.std(mse_scores)))
Congratulations, you've mastered it! Now, you know different validation strategies as well as how to use them to obtain overall model performance. It's time for the next and the most interesting part of the solution process: Feature Engineering and Modeling. See you in the next Chapters!